有1、2、3、4、5、6、10、12、15、20、30、60,共12个 。60因数的算法为:60=1×60=2×30=3×20=4×15=5×12=6×10 。因数是指能被这个数整除的数 。倍数是指能将这个数整除的数,因为60能被这些因数整除,所以60也叫做这些因数的倍数 。
群论在方程中的作用,就是它可以描述方程中的对称性 。
f(x) = x^3 + ax^2 + bx + c
= (x - x1)(x - x2)(x - x3)
= x^3 - (x1 + x2 + x3)x^2 + (x1x2 + x1x3 + x2x3)x - x1x2x3
= 0.
从上面的式子就可以获得根与系数的关系:
a = -(x1 + x2 + x3),
b = x1x2 + x1x3 + x2x3,
c = -x1x2x3,
以上是3次方程的韦达定理 。
如果是2次方程x^2 + ax + b = 0,就是人们熟知的a = -(x1 + x2), b = x1x2.
高次方程,实际上也一样 。
既然要求根,那么先假设根已经求出来了,然后展开1次因式的乘积,就可以获得根与系数的关系 。
1,韦达定理,关于根是对称的 。
n次多项式方程里的第n-1次项的系数,是所有根的和的相反数 。
3次方程里,这一项就是2次项 。
2次方程里,这一项就是1次项 。
常数项,是所有的根与(-1)^n的乘积,所以3次方程是c = -x1x2x3,而2次方程是b = x1x2:
(-1)^3 = -1, (-1)^2 = 1.
中间的第k项,都是从n个里任选k个根的乘积然后求和,前面的符号是(-1)^k.
对于3次方程来说,中间只有1项:
最高次项不算,从n-1次项开始计数,1次项在3次方程里是第2项,所以它是任选2个根的乘积然后求和 。

文章插图
从3个里选2个,与从3个里选1个是一样的,可能的选法都是3种 。
所以,3次方程的1次项系数是:(x1x2 + x2x3 + x1x3)(-1)^2 = x1x2 + x2x3 + x1x3.
韦达定理的所有式子,在交换根的次序的情况下,都是不变的!

文章插图
3次方程的韦达定理
也就是说,韦达定理对于根来说是对称的 。
2,方程是根的多元对称函数,
如果把方程不看做未知数的函数,而是看做根的函数,那么它是根的多元对称函数 。
f(x) = x^3 + ax^2 + bx + c
= x^3 - (x1+x2+x3)x^2 + (x1x2 + x2x3 + x1x3)x -x1x2x3
= F(x1, x2, x3)= 0.
任意改变F(x1, x2, x3)中的x1, x2, x3的次序,结果都是不变的,因为它除了乘积就是加法 。
如果有一个群G作用到根的下标上,那么F(x1, x2, x3)在G的作用下是不变的:

文章插图
群G的作用就是改变下标的次序,群G里的每个元素g都是一种改变方式 。
当方程是3次的时候,这种改变只有3! = 6种,也就是群G的元素个数只有6个!
当方程是5次的时候,这种改变有5! = 120种 。
群G的元素个数叫做它的阶,一般用绝对值的符号表示 。
当n = 5时,改变根的下标次序的这个群G的阶是:|G| = 5! = 120.
它与1, 2, 3, 4, 5的排列组合数是一样的,1,2,3,4,5的排列组合叫S5对称群 。
(1,2,3的排列组合,叫S3对称群)
像韦达定理这样的函数叫做对称函数 。
如果忽略掉符号(-1)^k,那么对称函数都是这样的:
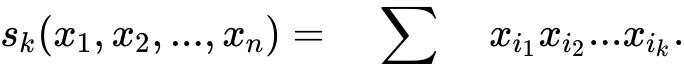
文章插图
右边是从n个里选k个不同的下标的所有可能乘积的求和 。
如果一个高次方程能够求根,那么它的根一定是这样的 。
所以,方程的系数,实际上是通过根的对称变化合成出来的 。
求根公式,就是把这种对称合成再返回去 。
要想通过求根公式把它返回去,那么合成系数的这个对称群,必须是可解群 。
这是伽罗瓦定理的要求 。
3,域的扩张与根的合成,
假设方程是(x - 2^0.5)(x - 3^0.5)(x - 5^0.5) = 0,那么展开之后它的系数是什么样的?
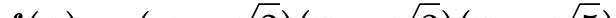
文章插图

文章插图
它在有理数Q上是多少维的向量空间?

文章插图
里的元素,如果用有理数的坐标表示的话,基是多少维的?
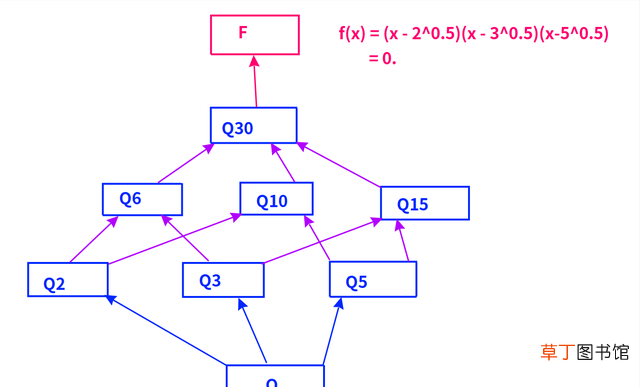
文章插图
多项式里的分裂域F(即包含方程的所有根的域)里的元素X,用有理数表示就是:

文章插图
如果不把15^0.5添加到Q里,有理数是没法合成出15^0.5的:
它是两个根 3^0.5 和 5^0.5,根据韦达定理的对称性合成出来的 。
合成的方式,就是在生成1次项的系数时,选择所有可能的2个根的乘积再求和,15^0.5是其中之一 。
伽罗瓦在1831年证明了,分裂域的子域与伽罗瓦群的子群是一一对应的:方程的可解对应着伽罗瓦群的可解(可以看我之前的文章) 。
伽罗瓦群与Sn对称群是同构的,它们要么都可解,要么都不可解 。
4,群的可解,
群G的可解,指的是有一条从G直到单位元e的、换位子群的导出链 。
G->G1->G2->...->Gn->e.
当有这么1条链的时候,群G对方程的根的作用,还可以变换回去 。
怎么选择的根合成的系数,再怎么把系数拆回到根,也就是根式求解 。
换位子群这个概念,是从乘法的交换律引出来的 。
群,是集合与集合上的“广义乘法”,而广义乘法不一定像数字乘法那样符合交换律 。
但是,群的单位元是符合交换律的:ae = ea,e是单位元 。
所以,只要有一条换位子群的链能够到达单位元,群里的广义乘法就可以返回去 。
这个“广义乘法”,在方程的求根问题上,就是根在合成系数时的排列组合 。
每一步,都相当于Sn对称群里的一个“广义乘法元素” 。
如果一个群的子集也是个群,就叫它的子群:因为群首先是个集合,其次是在集合上定义了乘法,最后是乘法要符合交换律、单位元、逆元、封闭 。
如果G是一个群,K是它的正规子群,那么G可解的充要条件是:K可解,同时G/K可解 。
(G/K,指的是属于G、但不属于K的元素组成的集合,叫商群)
正规子群的性质就是,aK = Ka,a属于G:也就是元素与它的乘法是符合交换律的 。
G的换位子群G',被包含在G的一个正规子群K里,并且G/G'是交换的 。
5,S5对称群不可解,
元素个数有限的群,叫有限群 。
拉格朗日证明了:有限群的阶(元素个数)能够被它的子群的阶整除 。
S5对称群有120个元素,它的子群A5交错群有60个元素,是它的一半 。
根据可解的充要条件,S5可解的前提是A5可解 。
柯斯特利金说的:A5除了单位元e之外,还包含15个2阶元(i j)(k j),20个3阶元(i j k),24个5阶元(1, i1, i2, i3, i4).
(i j)表示把标号i变成j,把j变成i,它的作用是把标号i和j对换,例如:
(1 2)x1 = x2,(1 2)x2 = x1.
(i j k)表示把标号按照 i->j->k->i 的顺序循环变换,例如:
(1 2 3)(x1 - x2) = x2 - x3,(1 2 3)(x2 - x3) = x3 - x1.
2个的就是对换,多个的就是循环 。
对换的就是交换群,循环的就是循环群,它们都是可解的 。
(有兴趣的可以拿着1, 2, 3, 4, 5的排列组合去验证下,是不是可以这么拆开)
根据拉格朗日定理,A5的阶是60,它的子群K必须是单位元、2阶元、3阶元、5阶元的组合,而且K的阶(即元素个数)必须整除60 。
也就是说,子群K的元素个数必须是60的因数,但不能是1和60!
如果是1,说明K是单位元e 。
如果是60,说明K就是父群A5 。
如果一个群的正规子群只有单位元e和它自身,那么它是不可解的,这叫单群:就跟素数17的因数只有1和17一样,它没法分解质因数 。
|K| = 1 + a x 15 + b x 20 + c x 12 + d x 12,(1表示单位元e).
24个5阶元分成12x2份,一个是(1 2 3 4 5),另一个是(1 2 3 5 4).
60的因数有:1,2,3,4,5,6,10,12,15,20,30,60 。
a = b = c = d = 0,对应的|K| = 1 。
a, b, c, d不全是0的时候:
1)a必须是1或3,因为只有15是奇数,其他的都是偶数 。
如果a = 3,那么剩下的是60 - 1 - 45 = 14,它没法被拆成20和12的组合,无解 。
所以a = 1,1 + 15 = 16.
2)超过16的因数只有20、30、60:
20 - 16 = 4,显然没法用20和12组合出来 。
30 - 16 = 14,显然也没法用20和12组合出来 。
60 - 16 = 44 = 1x20 + 2x12,但这么组合出来的 |K| = 60!
所以,A5不是可解群 。
所以,S5不是可解群 。
【5次方程中的对称与可解资料 60的因数有哪些数字】所以,一般5次方程没有根式解 。
推荐阅读
- 如何识别图片中的文字
- 表格中的数字变成了e+17怎么恢复
- 微信标签中的分组如何删除
- 梦见葡萄 梦见葡萄是什么意思
- 花生米药用价值有哪些
- 百发百中的故事 百发百中的成语典故
- 可在名字中的寓意是什么 可在名字中的寓意有哪些
- 稀硫酸与铁锈反应的化学方程式稀硫酸与铁锈反应的化学方程式是什么
- 盐酸与碳酸钙反应方程式 盐酸与碳酸钙反应化学方程式
- 表格家庭成员称谓怎么填